大家好，又见面了，我是你们的朋友全栈君。

本文利用跟踪微分器（TD）+ 扩张状态观测器（ESO）+ 非线性 PID 实现了受外扰的未知系统的控制，使得受控系统输出了期望的信号。

无超调，无震颤，参数好调节，堪称完美控制器！！！

什么是自抗扰控制

自抗扰技术的提出是为了解决PID控制技术的几个缺点:

1. 要求缓变的输出变量跟踪跳变的控制目标是不合理的;
2. 误差的微分信号不好提取, 易受噪声影响;
3. P、I、D的线性组合不是最优的组合方式;
4. 误差积分I的引入带来很多副作用, 比如使得闭环变得迟钝、产生震荡等.

针对以上问题, 在自抗扰控制中分别使用以下策略来克服:

1. 安排控制目标的“过渡过程”;
2. 使用跟踪微分器(Tracking Differentiator, TD)提取“微分”;
3. 寻找合适的非线性组合;
4. 使用扩张状态观测器来估计总扰动.

以上四点中, 1和3可以视为工程上的优化策略, 而2和4的核心技术都是跟踪微分器.

跟踪微分器的功能为: 输入信号$v(t)$, 输出$n$个信号$z_1(t),\dots ,z_n(t)$. 其中$z_1(t)$跟踪信号$v(t)$, 而$z_i(t)={\dot{z}}_{i-1}(t),i=2,3,\dots ,n$.

扩张状态观测器本质上也是一个跟踪微分器.

自抗扰控制中主要讨论的控制对象为受外扰的不确定对象:
$$x^{(n)}=f(x,\dot{x},\dots ,x^{(n-1)},t)+w(t)+u(t)$$其中$f(x,\dot{x},\dots ,x^{(n-1)},t)$为未知函数, $w(t)$为未知的外扰, $u(t)$为控制量.

通常把$x,\dot{x},\dots ,x^{(n-1)}$作为系统状态, 而扩张状态就是把$x^{(n)}$也视为系统状态.

若$y=x(t)$为观测量, 那么$\dot{x},\dots ,x^{(n)}$就是观测量的各阶导数. 利用跟踪微分器, 可以直接根据$y$将系统的各阶导数估计出来, 即实现了扩张状态的观测.

而估计出$x^{(n)}$等价于将系统的未知动态$f(x,\dot{x},\dots ,x^{(n-1)},t)$和外扰$w(t)$的总和估计出来了.

系统的未知动态和外扰之和称为总扰动.

在控制量$u(t)$中将系统的总扰动抵消, 配合误差反馈, 就实现了自抗扰控制.

龙格库塔

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def dxdt(F, X, t, h=1e-2):
    assert(len(F)==len(X))
    X = np.array(X)
    K1 = np.array([f(X, t) for f in F])
    dX = h*K1/2
    K2 = np.array([f(X+dX, t+h/2) for f in F]) 
    dX = h*K2/2
    K3 = np.array([f(X+dX, t+h/2) for f in F])
    dX = h*K3 
    K4 = np.array([f(X+dX, t+h) for f in F])

    dX = (K1 + 2*K2 + 2*K3 + K4)*h/6

    return dX, np.array([f(X, t) for f in F])

辅助函数

def sat(x, delta):
    return  x/delta if np.abs(x)<delta else np.sign(x)

def fal(x, alpha=0.5, delta=0.1):
    return  x/np.power(delta,1-alpha) if np.abs(x)<delta else np.power(np.abs(x), alpha)*np.sign(x)

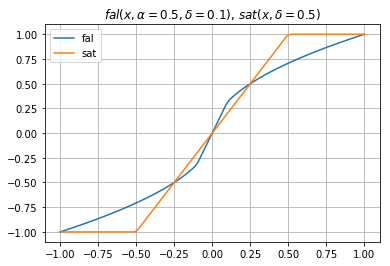
fal 函数具有小误差时高增益，大误差是低增益的特性，对抑制震颤发挥了重要作用。

跟踪微分器

期望输出为方波信号 $v(t)$

# target signal
def v(t):
    if t < 10:
        return np.sign(np.sin(0.8*t))  
    elif t < 20:
        return 2*(0.5*t-int(0.5*t)-0.5)
    else:
        return np.sin(0.8*t)

def v1(X, t):
    x1, x2 = X[0], X[1]
    return x2

def v2(X, t):
    x1, x2 = X[0], X[1]
    return -R*sat(x1 - v(t) + np.abs(x2)*x2/(2*R), delta)

扩张状态观测器

# eso
# 极点配置
p = np.poly1d([-15,-15,-15],True)
_, b1, b2, b3 = tuple(p.coef)

def g1(X, t):
    x1,x2,x3 = X[0], X[1], X[2]    
    return x2 - b1 * (x1 - y)  # y is model output

def g2(X, t):
    x1, x2, x3 = X[0], X[1], X[2]    
    return x3 - b2 * (x1 - y) + u

def g3(X, t):
    x1, x2, x3 = X[0], X[1], X[2]    
    return -b3 * (x1 - y)

未知真实状态

$$\ddot{x}=-x^3-x-0.2\dot{x}+w(t)+u(t)$$
其中 $w(t)$ 为外部扰动， $u(t)$ 为控制输入。

# hidden uncertain model
def f1(X, t):
    x, y = X[0], X[1]    
    return y

def f2(X, t):
    x, y = X[0], X[1]
    return -x*x*x - x -0.2*y + w(t) + u

def w(t):
    return 0.2 * np.sign(np.cos(t))  # perturbation

控制仿真

R = 90  # params in sal
delta = 0.001  # params in sal
h = 0.01  # discrete time unit
T = 20  # total time
N = int(T/h)  # num of points
V = [0., 0.]  # TD signal
X = [0., 0.]  # true state
Z = [0., 0., 0.]  # ESO 
u = 0  # initial control input
actual_output = []
expect_output = []
uncertain_dynamics = []
for i in range(N):
t = i*h  # time
dX, _ = dxdt([f1,f2],X,t,h)
X = X + dX
y = X[0]  # model output
dV, _ = dxdt([v1,v2],V,t,h)
V = V + dV
dZ, _ = dxdt([g1,g2,g3],Z,t,h)
Z = Z + dZ
e_p = V[0] - Z[0]
e_d = V[1] - Z[1]
fep, fed = fal(e_p), fal(e_d)
u = 10*fep + 50*fed - Z[2]
actual_output.append(y)
expect_output.append(V[0])
uncertain_dynamics.append(Z[2])
plt.plot(actual_output, color='black', label='output')
plt.plot(expect_output, color='red', linestyle='--',label='expect')
plt.plot(uncertain_dynamics, color='green', linestyle='--',label='uncertain state')
plt.legend(loc='lower right')
plt.show()

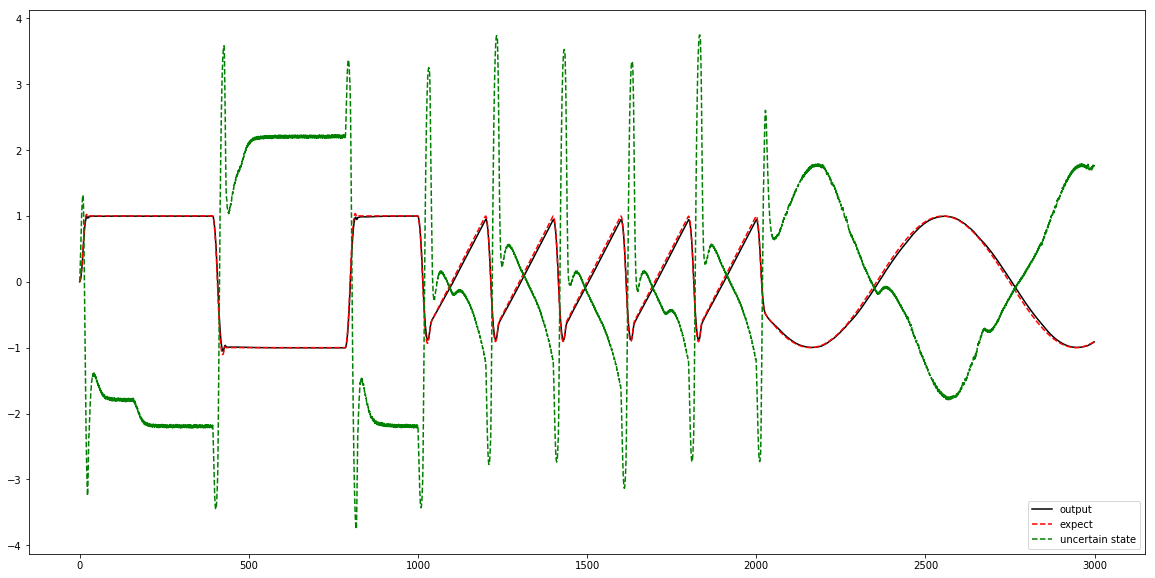
妈妈再也不用担心我调不好PID啦?