用python3实现粒子群优化算法（PSO）

大家好，又见面了，我是你们的朋友全栈君。

【注】：完整源码在我的github上，找不找得到就看自己咯 ^ _ ^

粒子群优化算法（Particle Swarm Optimization，PSO）属于进化算法的一种，是通过模拟鸟群捕食行为设计的。从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质。设想这样一个场景：一群鸟在随机搜索食物。在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
所有的粒子具有以下两个属性：速度、位置。
PSO 初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个”极值”来更新自己。第一个就是粒子本身所找到的最优解pbest。另一个极值是整个种群目前找到的最优解，即全局极值gbest。粒子通过下面的公式来更新自己的速度和位置：

速度：
$v_{i+1}=w\ast v_i+c_1\ast ran{d}_1\ast (pbes{t}_i-x_i)+c_2\ast ran{d}_2\ast (gbes{t}_i-x_i)$

位置：
$x_i=x_i+v_{i+1}$

以上两式中：
$w$为惯性因子，一般取1
$c_1、c_2$为学习因子，一般取2
$ran{d}_1、ran{d}_2$为两个（0,1）之间的随机数
$v_i和x_i$分别表示粒子第i维的速度和位置
$pbes{t}_i、gbes{t}_i$分别表示某个粒子最好位置第i维的值、整个种群最好位置第i维的值

注意：以上两式是针对粒子的某一维进行跟新的。对粒子的每一维，都要用上述的式子进行更新

说了这么多，下面把主要部分代码上上来（不上全是因为伸手党太多，哈哈）：

import numpy as np
import random

class PSO:
    def __init__(self, dim, size, iter_num, x_max, max_vel, best_fitness_value=float('Inf'), C1 = 2, C2 = 2, W = 1):
        self.C1 = C1
        self.C2 = C2
        self.W = W
        self.dim = dim  # 粒子的维度
        self.size = size  # 粒子个数
        self.iter_num = iter_num  # 迭代次数
        self.x_max = x_max
        self.max_vel = max_vel  # 粒子最大速度
        self.best_fitness_value = best_fitness_value
        self.best_position = [0.0 for i in range(dim)]  # 种群最优位置
        self.fitness_val_list = []  # 每次迭代最优适应值

        # 对种群进行初始化
        self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]

    # 更新速度
    def update_vel(self, part):
        for i in range(self.dim):
            vel_value = self.W * part.get_vel()[i] + self.C1 * random.random() * (part.get_best_pos()[i] - part.get_pos()[i]) \
                        + self.C2 * random.random() * (self.get_bestPosition()[i] - part.get_pos()[i])
            if vel_value > self.max_vel:
                vel_value = self.max_vel
            elif vel_value < -self.max_vel:
                vel_value = -self.max_vel
            part.set_vel(i, vel_value)

    # 更新位置
    def update_pos(self, part):
        for i in range(self.dim):
            pos_value = part.get_pos()[i] + part.get_vel()[i]
            part.set_pos(i, pos_value)
        value = fit_fun(part.get_pos())
        if value < part.get_fitness_value():
            part.set_fitness_value(value)
            for i in range(self.dim):
                part.set_best_pos(i, part.get_pos()[i])
        if value < self.get_bestFitnessValue():
            self.set_bestFitnessValue(value)
            for i in range(self.dim):
                self.set_bestPosition(i, part.get_pos()[i])

    def update(self):
        for i in range(self.iter_num):
            for part in self.Particle_list:
                self.update_vel(part)  # 更新速度
                self.update_pos(part)  # 更新位置
            self.fitness_val_list.append(self.get_bestFitnessValue())  # 每次迭代完把当前的最优适应度存到列表
        return self.fitness_val_list, self.get_bestPosition()

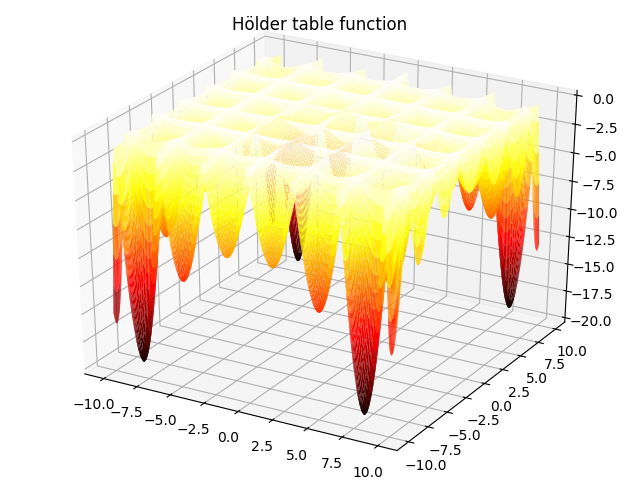
在上述代码中，跟粒子的速度设置了最大值，确保粒子速度的变化在某一范围内。接下来，我们可以用以上代码来进行测试了，这里测试用的是Hölder table function测试函数，在我的另一篇博客用python绘制评估优化算法性能的测试函数里有提到，其图像如下：

它的最优解有如下4个：

接下了我们通过以下代码进行测试：

from OptAlgorithm.PSO import PSO
import matplotlib.pyplot as plt
import numpy as np


dim = 2
size = 20
iter_num = 1000
x_max = 10
max_vel = 0.5

pso = PSO(dim, size, iter_num, x_max, max_vel)
fit_var_list, best_pos = pso.update()
print("最优位置:" + str(best_pos))
print("最优解:" + str(fit_var_list[-1]))
plt.plot(np.linspace(0, iter_num, iter_num), fit_var_list, c="R", alpha=0.5)
plt.show()

以上代码中，设置粒子维度为2维，种群大小即粒子个数为20，迭代次数为1000，粒子初始化的位置在（-10,10）之间，粒子的最大速度为0.5

以下是一次算法的收敛图像结果，：

打印的最优解和适应度如下：

可以看出其最优位置是函数四个最优解里面的一个，运行多次会出现不同的结果。甚至可能会得到如下图所示的函数收敛图像：

注意看此时函数的适应度在-9.5左右，继续迭代也没有发生变化，此时即陷入了局部最优。这篇博客主要介绍粒子群算法，这个情况这里就不继续讨论了。