大家好，又见面了，我是你们的朋友全栈君。
线程安全考虑三个方面：原子性，可见性，有序性
为什么使用voliate关键字？
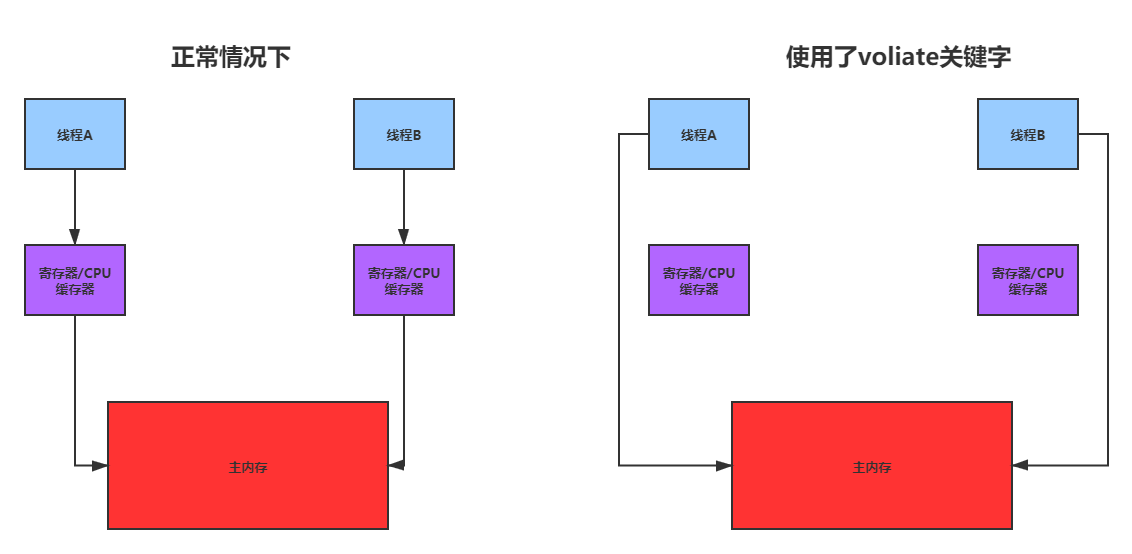
正常情况下编译器为了加快程序运行的速度,对一些变量的写操作会先在寄存器或者是CPU缓存上进行,最后才写入内存.而在这个过程,变量的新值对其他线程是不可见的.而volatile的作用就是使它修饰的变量的读写操作都必须在内存中进行!
- voliate和synchronized区别
- volatile本质是在告诉jvm当前变量在寄存器中的值是不确定的,需要从主存中读取,synchronized则是锁定当前变量,只有当前线程可以访问该变量,其他线程被阻塞住.
- volatile仅能使用在变量级别,synchronized则可以使用在变量,方法.
- volatile仅能实现变量的修改可见性,但不具备原子特性,而synchronized则可以保证变量的修改可见性和原子性.
- volatile不会造成线程的阻塞,而synchronized可能会造成线程的阻塞.
- volatile标记的变量不会被编译器优化,而synchronized标记的变量可以被编译器优化.
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
发布者：全栈程序员-用户IM，转载请注明出处：https://javaforall.cn/136335.html原文链接：https://javaforall.cn
【正版授权，激活自己账号】： Jetbrains全家桶Ide使用，1年售后保障，每天仅需1毛
【官方授权 正版激活】： 官方授权 正版激活 支持Jetbrains家族下所有IDE 使用个人JB账号...