大家好，又见面了，我是你们的朋友全栈君。

文章的目的

我们经常需要对一些企业、部门、甚至某个城市进行评价，但是用一个指标不可能全面反映这些复杂单元，所以我们经常会用很多指标进行评价，这些指标单位不统一，大小数量级有时候相差很多，把这些复杂的指标最后综合起来成为一个指数，这就是综合评分的本质。综合评价的方法有很多，主要有三类：主观综合评价、客观综合评价、主客观混合评价。本文主要是讲述客观综合平台里的变异系数法。本文有两个目标：

各个指标权重的确定

多个单元的排序（竞争力排名、大学排名、发展水平、幸福排名、税负排名诸如此类）

变异系数法的计算过程

每个城市的评价我们保留了10个指标，首先是要知道哪个指标最重要，一个人身上身上有很多伤口，有刀伤、钝器伤害、拳头打的印子，到底哪个是最致命的！我们把这种重要性的不同称为权重。所以第一件事就是确定10个指标的权重分别是多少。原理这里不谈，我们只谈下计算过程。

导入数据并做初步处理

import matplotlib.pyplot as plt  # 第1-3行代码是读入数据的时候，在Python不会产生中文乱码
plt.rcParams['font.sans-serif'] = ['microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
import pandas as pd  # 第4-5行代码是两个数据分析有名的库，也可以称为工具吧
import numpy as np
from xlwt import *  # 这是把最后的数据结果写入excel的库
data = pd.read_excel('D:\\5.python data\\airports.xls')  # 把指定位置的excel表格数据导入python形成一个dataframe表格数据，Pd是pandas的简称，这个工具把excel中的数据读入Python中，形成一个称作dataframe的表格，正常的路径是D:\5.python data\airports.xls，但是在python中很容易产生冲突，就把“\”改成了‘\\’.excel中的表要像开始阐述的那样排列。
print(data)  # 观察导入的数据表格，如这种类型格式的数据才能导入计算。导入后如下：
 city    GDP：亿元    人口（万）  ...  进出口总值（亿元）  旅客吞吐量（万人次）  货邮吞吐量（万吨）
0   广州  21503.15  1449.84  ...    9714.36     6583.69   233.8500
1   深圳  22438.39  1252.83  ...   28075.33    18142.24   115.9000
2   珠海   2564.73   176.54  ...    3001.10      921.68     3.7400
3   佛山   9549.60   765.67  ...    4358.24     4929.00     0.0242
4   惠州   3830.58   477.70  ...    3419.77       95.69     0.4000
5   香港  22160.67   741.31  ...   71642.32     5665.50   493.8000
6   澳门   3406.55    65.31  ...     736.42      716.00     3.7000`![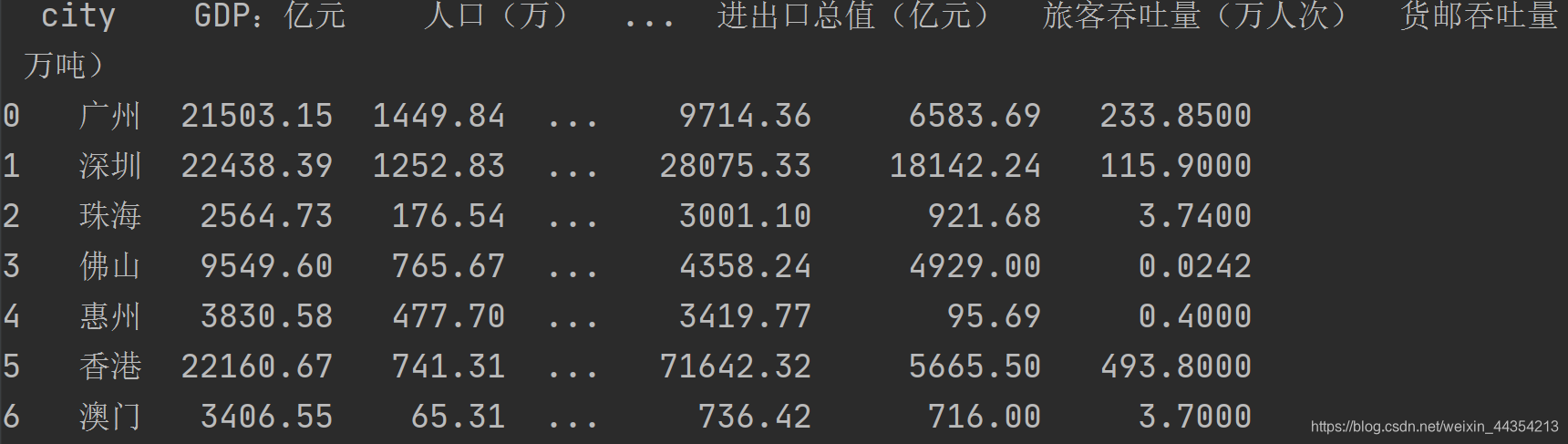
这里一共10个指标，只显示了5个，中间5个由...号代替](https://img-blog.csdnimg.cn/20200725202418189.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM1NDIxMw==,size_16,color_FFFFFF,t_70)
``
由于第一列是city,城市不参加计算，所以要去掉这一列，代码如下

del data[list(data)[0]] # 第一列是城市，不参加求均值、标准差、变异系数的过程，所以先删掉
print(data)

结果如下

 GDP：亿元    人口（万）  城镇化率（%）  ...  进出口总值（亿元）  旅客吞吐量（万人次）  货邮吞吐量（万吨）

0 21503.15 1449.84 86.14 … 9714.36 6583.69 233.8500
1 22438.39 1252.83 100.00 … 28075.33 18142.24 115.9000
2 2564.73 176.54 89.37 … 3001.10 921.68 3.7400
3 9549.60 765.67 94.00 … 4358.24 4929.00 0.0242
4 3830.58 477.70 68.15 … 3419.77 95.69 0.4000
5 22160.67 741.31 100.00 … 71642.32 5665.50 493.8000
6 3406.55 65.31 100.00 … 736.42 716.00 3.7000

数据的归一化

我们观察这10个指标，第一个是GDP，单位是亿元，广州GDP数字是吓人的21503亿，是马巴巴财富的10倍多，这是比较大的，最小的是城镇化率，同样是广州，是86.14%，也就是0.8614，和GDP相比完全是小蚂蚁，可以忽略不计，但是能忽略不，回答是不能！为了规避这种数量级的影响，我们要把数据全部化成一个0-1之间的数，这样比较才公平。这就是归一化，归一化的手段很多，常用的是简单归一化和标准化归一化，而标准化归一化适用于那些样本数据很大的，和本文不相匹配，没有最好，适合的就是最好的。公示很简单
我们任意取一个城市的GDP，看其归一值怎么求，这几个城市里面我呆过比较时间长的是广州，但我更喜欢珠海，一个176.54万人口的美丽滨海城市，有大大小小100多个岛屿，我很喜欢东奥岛，回归正题，我们就计算珠海GDP的归一值吧
公式：
珠海的GDP归一值=（珠海的GDP-7个城市GDP的最小值）/（7个城市GDP的最大值-7个城市GDP的最小值）=（珠海的GDP-7个城市GDP的最小值）/（7个城市GDP的最大值-7个城市GDP的最小值），很尴尬的是，珠海的GDP就是7个城市中的最小值，所以其归一值为0！
通过这样的算法，把7*10个数据全部化成0-1之间的值，代码如下：

# 假设上面有一个DataFrame叫做data
GYH = (data-data.min())/(data.max()-data.min())  # 即实现简单标准化归一
print(GYH)  # 归一之后的表格，GYH是归一化的中文缩写

GDP：亿元     人口（万）   城镇化率（%）  ...  进出口总值（亿元）  旅客吞吐量（万人次）  货邮吞吐量（万吨）

0 0.952941 1.000000 0.564835 … 0.126618 0.359515
1 1.000000 0.857706 1.000000 … 0.385566 1.000000
2 0.000000 0.080338 0.666248 … 0.031939 0.045770
3 0.351464 0.505847 0.811617 … 0.051079 0.267825
4 0.063695 0.297856 0.000000 … 0.037844 0.000000
5 0.986026 0.488252 1.000000 … 1.000000 0.308636
6 0.042359 0.000000 1.000000 … 0.000000 0.034373
为了显示好看更好说明问题，把最后一列的归一化值省略了！

求每个指标的平均值与标准差

例如GDP归一化之后7个城市的平均值，代码

#  求相关列均值与标准差
GYHLJZ = GYH.mean(axis=0)  # axis=0,求各列的均值；axis=1，求各行的均值
# print(GYHLJZ)
GYHlBZC = GYH.std(ddof=0)  # ddof=0求标准差时除以n，如果是ddof=1时除以n-1
# print(GYHBZC)

求每个指标的变异系数，求10个指标变异系数的和

# 求变异系数
GYHlBYXS = GYHlBZC/GYHLJZ  # 变异系数=标准差/平均值
# print(GYHLBYXS)

# 对变异系数求和
GYHLBYXSDH = GYHlBYXS.sum()
# print(GYHLBYXSDH)

求每个指标的权重

# 得出权重
QZ = GYHlBYXS/GYHLBYXSDH  # 用变异系数除以所有变异系数之和得出权重矩阵
print(QZ)

到此为止，我们已经完成了任务目标1：求每个指标的权重，从中发现谁对城市的竞争力或发展水平影响最大。请看结果。
GDP：亿元 0.092432
人口（万） 0.076098
城镇化率（%） 0.047389
失业人员（万） 0.118713
财政收入（亿元） 0.106368
固定资产投资（亿元） 0.059396
社会消费品零售总额（亿元） 0.095863
进出口总值（亿元） 0.146315
旅客吞吐量（万人次） 0.113138
货邮吞吐量（万吨） 0.144289
结果在我们意料之中，也感觉有点意外，影响最大的是进出口总值，权重是10个指标中最大的0.146315，意外的是排第二、第三、第四的是货邮吞吐量、失业人口、旅客吞吐量，如果是本科生文章，写到已经是一篇很好的文章，你找到了影响一个城市最重要的因素，也就是你有了努力的方向，然后把这些方向的优缺点摆出来，然后总结出几个可以行的通的政策建议，妥妥的一篇好文章。

计算城市的排名

权重已经找出来了，但是城市的排名还是没有出来，革命还未成功，同志还需努力！！！
如何计算排名，首先要我们要把归一化后表GYH中的值和刚刚求得的权重相乘，GYH是一个7行10列的表格，QZ是一个1行10列的表格，所以这两个相乘首先要把他们两个都转化成矩阵，然后GYH和QZ转置矩阵相乘，得到一个7行1列的表格，实际就是7个城市分别得到一个值。

#  将权重（QZ表格）转换为矩阵
QZJZ = np.mat(QZ)  # 因为涉及到两个dataframe的值相乘，需要先转化为矩阵，首先把权重转化为矩阵
print(QZJZ)
#  将GYH表格转换为矩阵
GYHJZ = np.mat(GYH)  # 把归一化后的数据转化为矩阵
# print(GYHJZ)
#  归一化矩阵乘以转置的权重矩阵得到一个7行1列的矩阵
NZHPFJZ = GYHJZ * QZJZ.T  # 矩阵相乘，要注意第一个矩阵的列和第二个矩阵的行必须一致，.T代表矩阵的转置
NZHPF = pd.DataFrame(NZHPFJZ.T)  # 把相乘后的矩阵转化为dataframe
# print(NZHPF)

计算每个城市的得分

每个城市已经计算出来一个数字，为了更好的比较，还要归一化一次。因为现在只有一列，归一化比较容易计算。

#  累加每个城市的得分求和得到总分
NZHPFZH = list(NZHPF.apply(sum))
# print(NZHPFZH)
#  max-min依然简单 归一化（如果要研究城市竞争力和另一个变量之间的关系，数据算到归一化之前就OK，如何只研究城市竞争力本身的排名，要继续归一化
NZHPFZH = pd.DataFrame(NZHPFZH)  # 把矩阵变成dataframe表格，矩阵不能归一化
ZHPFGYH = (NZHPFZH-NZHPFZH.min())/(NZHPFZH.max()-NZHPFZH.min())
# print(ZHPFGYH)
# 城市的热度值映射成分数（0-100分）
result = ZHPFGYH*100
print(result)

0 83.945155
1 100.000000
2 0.662802
3 23.996897
4 1.631386
5 92.625916
6 0.000000
按照这10个指标综合评价，广州得分最高100分，最低分是澳门，但是这是只是为介绍变异系数法进行综合评价，指标没有不全面，结果和现实有出入，主要学习这种计算方法。
总结：实际是一个傻瓜式的计算，你把收集的数据足够丰富、数据正确，格式正确，输入进去，就会把指标的权重和排名帮你计算出来。最后，把代码全部奉上。

# -*- encoding=utf-8 -*-
# ==================================
# 1、数据的归一化（可以最大最小归一，也可以标准化归一）
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from xlwt import *
plt.rcParams['font.sans-serif'] = ['microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
data = pd.read_excel('D:\\5.python data\\airports.xls')  # 把指定位置的excel表格数据导入python形成一个dataframe表格数据
print(data)  # 观察导入的数据表格，如这种类型格式的数据才能导入计算
del data[list(data)[0]]  # 第一列是年份，不参加求均值、标准差、变异系数的过程，所以先删掉
print(data)
# 假设上面有一个DataFrame叫做data
GYH = (data-data.min())/(data.max()-data.min())  # 即实现简单标准化归一
print(GYH)  # 归一之后的表格
# BZGYH = (data-data.mean())/(data.std())  # data.mean()是平均值、data.std()是标准差
#  求相关列均值与标准差
GYHLJZ = GYH.mean(axis=0)  # axis=0,求各列的均值；axis=1，求各行的均值
# print(GYHLJZ)
GYHlBZC = GYH.std(ddof=0)  # ddof=0求标准差时除以n，如果是ddof=1时除以n-1
# print(GYHBZC)
# 求变异系数
GYHlBYXS = GYHlBZC/GYHLJZ  # 变异系数=标准差/平均值
# print(GYHLBYXS)
# 对变异系数求和
GYHLBYXSDH = GYHlBYXS.sum()
# print(GYHLBYXSDH)
# 得出权重
QZ = GYHlBYXS/GYHLBYXSDH  # 用变异系数除以所有变异系数之和得出权重矩阵
print(QZ)
#  将权重（QZ表格）转换为矩阵
QZJZ = np.mat(QZ)  # 因为涉及到两个dataframe的值相乘，需要先转化为矩阵，首先把权重转化为矩阵
print(QZJZ)
#  将GYH表格转换为矩阵
GYHJZ = np.mat(GYH)  # 把归一化后的数据转化为矩阵
# print(GYHJZ)
#  权重矩阵乘以归一化矩阵
NZHPFJZ = GYHJZ * QZJZ.T  # 矩阵相乘，要注意第一个矩阵的列和第二个矩阵的行必须一致，.T代表矩阵的转置
NZHPF = pd.DataFrame(NZHPFJZ.T)  # 把相乘后的矩阵转化为dataframe
# print(NZHPF)
#  累加求和得到总分
NZHPFZH = list(NZHPF.apply(sum))
# print(NZHPFZH)
#  max-min 归一化（如果要研究两个变量之间的关系，数据算到上一步就OK，如何研究数据本身的排名，继续
NZHPFZH = pd.DataFrame(NZHPFZH)
ZHPFGYH = (NZHPFZH-NZHPFZH.min())/(NZHPFZH.max()-NZHPFZH.min())
# print(ZHPFGYH)
#  部落的热度值映射成分数（0-100分）
# last_hot_score_result = [i * 100 for i in last_hot_score_autoNorm]
# print(last_hot_score_result)
result = ZHPFGYH*100
print(result)
# 数据保存进excel中
QZ.to_csv('D:\\5.python data\\jzl.csv', index=False, header=False, mode='a')  # index=False代表不要列头；header=False代表不要索引；mode='a'代表数据是追加写入不是覆盖
# NZHPF.to_csv('D:\\5.python data\\jzl.csv', index=False, mode='a')
result.to_csv('D:\\5.python data\\jzl.csv', index=False, header=False, mode='a')