大家好，又见面了，我是你们的朋友全栈君。

该文已经收录到专题机器学习进阶之路当中，欢迎大家关注。

1.过拟合

当样本特征很多，样本数相对较少时，模型容易陷入过拟合。为了缓解过拟合问题，有两种方法：

方法一：减少特征数量（人工选择重要特征来保留，会丢弃部分信息）。

方法二：正则化（减少特征参数的数量级）。

2.正则化（Regularization）

正则化是结构风险（损失函数+正则化项）最小化策略的体现，是在经验风险（平均损失函数）上加一个正则化项。正则化的作用就是选择经验风险和模型复杂度同时较小的模型。

防止过拟合的原理：正则化项一般是模型复杂度的单调递增函数，而经验风险负责最小化误差，使模型偏差尽可能小经验风险越小，模型越复杂，正则化项的值越大。要使正则化项也很小，那么模型复杂程度受到限制，因此就能有效地防止过拟合。

3.线性回归正则化

正则化一般具有如下形式的优化目标：

$\ mathop {\ min} \ limits_ {f \ in F} \ left [{\ frac {1} {m} \ sum \ limits_ {i = 1} ^ m {L \ left（{{y_i}，f \ left （{{x_i}} \ right）} \ right）} + \ lambda J \ left（f \ right）} \ right]$ （1）

其中， $\ lambda \ geq 0$ 是用来平衡正则化项和经验风险的系数。

正则化项可以是模型参数向量的范数，经常用的有范数，范数（范数： ${\左\ | x \ right \ | _1} = \ sum \ limits_ {i = 1} ^ m {\ left | {{x_i}} \ right |}$ ，范数: ${\左\ | x \ right \ | _2} = \ sqrt {\ sum \ limits_ {i = 1} ^ m {x_i ^ 2}}$ ) 。

我们考虑最简单的线性回归模型。

给定数据集 $D = \left\{ \left( x _ { i } , y _ { i } \right) \right\} _ { i = 1 } ^ { m }$ ，其中， $x _ { i } = \left( x _ { i 1 } , x _ { i 2 } , \dots , x _ { i d } \right)$ ， $y _ { i } \in R$ 。

代价函数为： $J \ left（w \ right）= \ frac {1} {m} {\ left \ | {y - {w ^ T} X} \ right \ | ^ 2} = \ frac {1} {m} \ sum \ limits_ {i = 1} ^ m {{{left（{{y_i} - {w ^ T} {x_i}} \ right）} ^ 2}}$ （2）

（1）范数正则化（Ridge Regression，岭回归）

代价函数为：

（2）范数正则化（LASSO，Least Absoulute Shrinkage and Selection Operator，最小绝对收缩选择算子）

代价函数为：

（3）正则项正则项结合（Elastic Net）

代价函数为：

$J \ left（w \ right）= \ frac {1} {m} \ sum \ limits_ {i = 1} ^ m {{{\ left（{{y_i} - {w ^ T} {x_i}} \ right }} ^ 2}} + \ lambda \ left（{\ rho {{\ left \ | w \ right \ |} _1} + \ left（{1 - \ rho} \ right）\ left \ | w \ right \ | _2 ^ 2} \ right）$ （5）

其中，范数正则化、范数正则化都有助于降低过拟合风险，范数通过对参数向量各元素平方和求平方根，使得范数最小，从而使得参数的各个元素接近0 ，但不等于0。 而范数正则化比范数更易获得“稀疏”解，即范数正则化求得的会有更少的非零分量，所以范数可用于特征选择，而范数在参数规则化时经常用到（事实上，范数得到的“稀疏”解最多，但范数 $\左\ | x \ right \ | = \＃\ left（{i \ left | {{x_i} \ ne 0} \ right。} \ right）$ 是中非零元素的个数，不连续，难以优化求解。因此常用范数来近似代替）。

为什么正则化更易获得“稀疏”解呢？

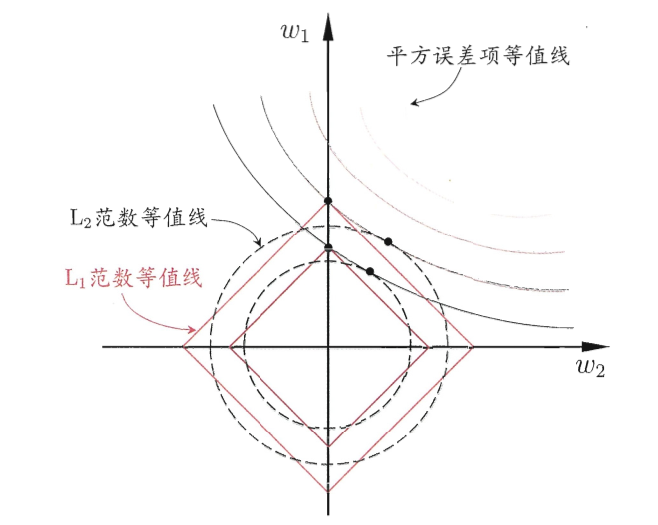
假设仅有两个属性，只有两个参数 ${W_1}，{W_2}$ ，绘制不带正则项的目标函数-平方误差项等值线，再绘制，范数等值线，如图1正则化后优化目标的解要在平方误差项和正则化项之间折中，即出现在图中等值线相交处采用。范数时，交点常出现在坐标轴上，即或为0;而采用范数时，交点常出现在某个象限中，即，均非0。也就是说，范数比范数更易获得“稀疏”解。

4.岭回归求解

岭回归不抛弃任何一个特征，缩小了回归系数。

岭回归求解与一般线性回归一致。

（1）如果采用梯度下降法：

$\ frac {{\ partial J \ left（w \ right）}} {{\ partial {w_j}}} = \ frac {1} {m} \ sum \ limits_ {i = 1} ^ m {\ left（{ {w ^ T} {x_i} - {y_i}} \ right）{x_ {ij}} + 2 \ lambda {w_j}}$ （6）

迭代公式如下：

$\ begin {array} {l} {w_ {j + 1}} = {w_j} - \ frac {\ alpha} {m} \ sum \ limits_ {i = 1} ^ m {\ left（{{w ^ T } {x_i} - {y_i}} \ right）{x_ {ij}} - 2 \ lambda {w_j}} \\ = \ left（{1 - 2 \ lambda} \ right）{w_j} - \ frac {\ alpha} {m} \ sum \ limits_ {i = 1} ^ m {\ left（{{w ^ T} {x_i} - {y_i}} \ right）{x_ {ij}}} \ end {array}$ （7）

（2）如果采用正规方程：

最优解为：

${w ^ *} = {\ left（{{X ^ T} X + \ lambda I} \ right）^ { - 1}} {X ^ T} y$ （8）

最后，将学得的线性回归模型为：

$\ widehat y = {w ^ T} X = {X ^ T} w = {\ left（{{X ^ T} X + \ lambda I} \ right）^ { - 1}} {X ^ T} y$ （9）

5. LASSO回归求解

由于范数用的是绝对值，导致LASSO的优化目标不是连续可导的，也就是说，最小二乘法，梯度下降法，牛顿法，拟牛顿法都不能用。

正则化问题求解可采用近端梯度下降法（Proximal Gradient Descent，PGD）。

（1）优化目标

优化目标为： $\ mathop {\ min} \ limits_x \ left [{f \ left（x \ right）+ \ lambda {{\ left \ | x \ right \ |} _1}} \ right$ （10）

若 ${f \ left（x \ right）}$ 可导，梯度 $\ nabla f \ left（x \ right）$ 满足L-Lipschitz条件（利普希茨连续条件），即存在常数 $\压裂{{\左\ | {\ nabla f \ left（{x'} \ right） - \ nabla f \ left（x \ right）} \ right \ | _2 ^ 2}} {{\ left \ | {x' - x} \ right \ | _2 ^ 2}} \ le L，\ forall \ left（{x，x'} \ right）$ （11）

L-Lipschitz（利普希茨连续条件）定义：

对于函数 $f \ left（x \ right）$ ，若其任意定义域中的, 都存在 $\左| {f \ left（{{x_1}} \ right） - f \ left（{{x_2}} \ right）} \ right | \ le L \ left | {{x_1} - {x_2}} \ right |$ ，即对于 $f \ left（x \ right）$ 上每对点，连接它们的线的斜率的绝对值总是不大于这个实数。

（2）泰勒展开

在处将 $f \ left（x \ right）$ 进行二阶泰勒展开：

$f \ left（x \ right）= f \ left（{{x_k}} \ right）+ \ nabla f \ left（{{x_k}} \ right）\ left（{x - {x_k}} \ right）+ \ frac {{f''\ left（{{x_k} + \ xi} \ right）}} {2} {\ left（{x - {x_k}} \ right）^ 2}$ （12）

由（11）式，泰勒将展开式的二阶导用代替，得到：

$f \ left（x \ right）\ approx f \ left（{{x_k}} \ right）+ \ nabla f \ left（{{x_k}} \ right）\ left（{x - {x_k}} \ right） + \ frac {L} {2} {\ left（{x - {x_k}} \ right）^ 2}$ （13）

（3）简化泰勒展开式

将（13）式化简：

$\ begin {array} {l} f \ left（{{x_k}} \ right）+ \ nabla f \ left（{{x_k}} \ right）\ left（{x - {x_k}} \ right）+ \ frac {L} {2} {\ left（{x - {x_k}} \ right）^ 2} \\ = \ frac {L} {2} \ left [{{{{left（{x - {x_k} } \ right）} ^ 2} + \ frac {2} {L} \ nabla f \ left（{{x_k}} \ right）\ left（{x - {x_k}} \ right）+ \ frac {1} {{{L ^ 2}}} {{\ left（{\ nabla f \ left（{{x_k}} \ right）} \ right）} ^ 2}} \ right] - \ frac {L} {2} \ frac {1} {{{L ^ 2}}} {\ left（{\ nabla f \ left（{{x_k}} \ right）} \ right）^ 2} + f \ left（{{x_k}} \ right）\\ = \ frac {L} {2} {\ left [{x - \ left（{{x_k} - \ frac {1} {L} \ nabla f \ left（{{x_k}} \ right }} \ right）} \ right] ^ 2} + \ varphi \ left（{{x_k}} \ right）\\ = \ frac {L} {2} \ left \ | {x - \ left（{{x_k} - \ frac {1} {L} \ nabla f \ left（{{x_k}} \ right）} \ right）} \ right \ | _2 ^ 2 + \ varphi \ left （{{x_k}} \ right）\ end {array}$ （14）

其中， $\ varphi \ left（{{x_k}} \ right）{\ rm {=}} f \ left（{{x_k}} \ right） - \ frac {1} {{2L}} {\ left（{\ nabla f \ left（{{x_k}} \ right）} \ right）^ 2}$ 是无关的常数。

（4）简化优化问题

这里若通过梯度下降法对 $f \ left（x \ right）$ （ $f \ left（x \ right）$ 连续可导）进行最小化，则每一步下降迭代实际上等价于最小化二次函数 $\ widehat f \ left（x \ right）$ ，推广到优化目标（10），可得到每一步迭代公式：

${x_ {k + 1}} = \ mathop {\ arg \ min} \ limits_x \ left [{\ frac {L} {2} \ left \ | {x - \ left（{{x_k} - \ frac {1} {L} \ nabla f \ left（{{x_k}} \ right）} \ right）} \ right \ | _2 ^ 2 + \ lambda {{ \左\ | x \ right \ |} _1}} \ right]$ （15）

令 $z = {x_k} - \ frac {1} {L} \ nabla f \ left（{{x_k}} \ right）$ ，

则可以先求，再求解优化问题：

${x_ {k + 1}} = \ mathop {\ arg \ min} \ limits_x \ left [{\ frac {L} {2} \ left \ | {x - z} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | x \ right \ |} _1}} \ right]$ （16）

（5）求解

令为的第个分量，将（16）式按分量展开，其中不存在 $x ^ ix ^ j（i \ neq j）$ 这样的项，即的各分量之间互不影响，所以（12）式有闭式解。

为什么（16）式不存在 $x ^ ix ^ j（i \ neq j）$ 这样的项？

因为展开（16）式得到， $\ begin {array} {l} \ mathop {\ arg \ min} \ limits_x \ left [{\ frac {L} {2} \ left \ | {x - z} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | x \ right \ |} _1}} \ right] \\ = \ mathop {\ arg \ min} \ limits_x \ left（{\ frac {L} {2} \ left \ | {{x ^ 1} - {z ^ 1}} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | {{x ^ 1}} \ right \ |} _1}} \ right）+ \ mathop {\ arg \ min} \ limits_x \ left（{\ frac {L} {2} \ left \ | {{x ^ 2} - {z ^ 2}} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | {{x ^ 2} } \ right \ |} _1}} \ right）+ \ cdots \\ + \ mathop {\ arg \ min} \ limits_x \ left（{\ frac {L} {2} \ left \ | {{x ^ d} - {z ^ d}} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | {{x ^ d}} \ right \ |} _1}} \ right）\ end {array}$

从而优化问题变为求解个独立的函数： $f \ left（x \ right）= {\ left（{x - z} \ right）^ 2} + \ lambda {\ left \ | x \ right \ | _1}$ 。

对于上述优化问题需要用到soft thresholding软阈值函数（证明见参考文献2），即对于优化问题：

$\ mathop {\ arg \ min} \ limits_x \ left [{\ left \ | {x - z} \ right \ | _2 ^ 2 + \ lambda {{\ left \ | x \ right \ |} _1}} \ right]$ （17）

其解为： $pro {x_u} \ left（z \ right）= sign \ left（z \ right）\ max \ left \ {{\ left | z \ right | - 你，0} \ right \}$ （18）

而我们的优化问题为（16）式，则得到闭式解为：

（19）

其中， $x_ {k + 1} ^ i$ 与分别是 $x_ {k + 1}$ 与的第个分量。因此，通过PGD能使LASSO和其他基于范数最小化的方法得以快速求解。

参考文献：

1.《机器学习》第十一章嵌入式选择与L1正则化——周志华

2. LASSO回归与L1正则化西瓜书

3. 机器学习之正则化（正规化）

4. 正则化及正则化项的理解

发布者：全栈程序员-用户IM，转载请注明出处：https://javaforall.cn/132576.html原文链接：https://javaforall.cn

【正版授权，激活自己账号】： Jetbrains全家桶Ide使用，1年售后保障，每天仅需1毛

【官方授权正版激活】： 官方授权正版激活支持Jetbrains家族下所有IDE 使用个人JB账号...

【机器学习】一文读懂正则化与LASSO回归，Ridge回归

1.过拟合

2.正则化（Regularization）

3.线性回归正则化

4.岭回归求解

5. LASSO回归求解

发表回复

【机器学习】一文读懂正则化与LASSO回归，Ridge回归

1.过拟合

2.正则化（Regularization）

3.线性回归正则化

4.岭回归求解

5. LASSO回归求解

相关推荐

原码反码补码的相互转换_补码转化为反码

华为云搭建MQTT服务器

用js写简单选项卡

怎么关闭eslint

如何开启默认共享(win7默认共享文件夹位置)

cmd无法切换目录_cmd重置目录

发表回复